Ist Ihnen bewusst dass um die Hälfte mehr von einem Betrag immer umgekehrt um ein Drittel weniger von dem nun größeren Betrag bedeutet. Das ist zwar plausibel und nachvollziehbar, ich kann aber nicht sagen dass mir das schon immer bewusst war, dass man es auf diesen einfachen Punkt bringen kann.

Wenn ich etwa in meinem Beispiel für den Drehmomentvergleich beim Benzinmotor 6000 U/min Nenndrehzahl annehme so ist das um die Hälfte (bzw. 50%) mehr als die 4000 U/min die ich beim Dieselmotor als Nenndrehzahl annehme. Umgekehrt dagegen sind die 4000 U/min des Dieselmotors um ein Drittel (33 %) weniger als die 6000 U/min des Benzinmotors.
Das Verhältnis der beiden Zahlen ist dagegen das gleiche, man muss mit 1,5 multiplizieren bzw. durch 1,5 dividieren.





Das ist, wie gesagt, auch völlig plausibel. Wenn ich zwei Teile von etwas habe und ich gebe ein Teil dazu so erhalte drei Teile, das ist um die Hälfte mehr als die zwei Teile die ich vorher hatte. Gebe ich von den nun drei Teilen einen Teil weg so sind die nun zwei Teile um ein Drittel weniger als die drei Teile vorher.
Wenn man also zu irgend etwas die Hälfte dazu gibt, so ist das umgekehrt von dem größeren Wert um ein Drittel weniger.

Das stimmt analog natürlich auch für jedes andere Verhältnis.
Vier ist um ein Drittel mehr als drei. Drei ist um ein Viertel weniger als Vier.
Um ein Drittel mehr von einem Betrag heißt also umgekehrt ein Viertel weniger von dem dann größeren Betrag. Der Faktor ist hier 1,33.

Oder z.B ein Neunundneunzigstel mehr von einem Betrag ist um ein Hundertstel weniger vom größeren Betrag.

Aufgefallen ist mir das übrigens vor langer Zeit beim Umrechnen der Leistung von kW in PS. Wenn man kW in PS (Faktor 1,36) umrechnet so ergibt das in PS rund um ein Drittel mehr. Bei Umrechnung von PS in kW (Faktor 0,736) ergibt das um rund ein Viertel weniger.

Als Zahlen kann man es noch folgendermaßen schreiben:

usw.
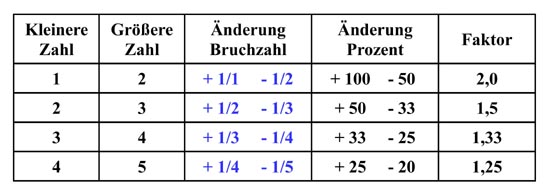
Für die kleinere und größere Zahl kann man natürlich jedes beliebige Vielfache davon einsetzen.

Rein theoretisch kann man es erweitern um z.B. um 2/3 mehr usw. Das ergibt aber eigentlich nichts was man im Alltag brauchen kann:


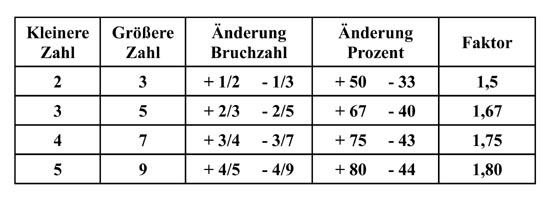
Oder um ein Vielfaches mehr, was aber auch nichts für den Alltag brauchbares ergibt:


Um die Hälfte mehr und um ein Drittel weniger ist zwar auch nicht eine neue Erkenntnis, das Bewusstsein dafür kann aber mitunter durchaus brauchbar sein.
Unter Umständen kann es zur Vermeidung von Missverständnissen beitragen.




Verwandtes Thema:

Was ist an der Zahl Zwölf besonderes?


Startseite


Copyright © 2017      Gottfried Langmann                            20.1.2017      aktualisiert:   1.2.2018