Wie erklärt sich eigentlich die optische Täuschung beim bekannten Wasserfall?
Im Prinzip denkbar einfach und zwar durch die Projektion eines dreidimensionalen Objekts auf ein zweidimensionales Bild.

Bild 1
Im vorherigen Bild 1 ist im linken Achsenkreuz die dritte Dimension vorne-hinten eingetragen. Nur diese vorne-hinten Achse kann natürlich genauso ein Pfeil zwischen der oben-unten Achse und der links-rechts Achse in der Ebene des Bildes sein, wie es im rechten Achsenkreuz dargestellt ist. Ob dies jetzt eine Projektion von vorne-hinten in die Bild-Ebene ist oder einfach ein Pfeil in der Bild-Ebene, kann man rein aufgrund der Linie nicht sagen. Es hängt von der Umgebung ab.
Beim bekannten Wasserfall ist es so dargestellt dass man aufgrund des umgebenden Mauerwerks und des fließenden Wassers eindeutig den Eindruck hat dass das Wasser von vorne nach hinten fließt. Man muss jetzt nur noch das Wasser von rechts nach links führen wie es mit der blauen strichlierten Linie im folgenden Bild 2 links dargestellt ist und schon ist man über dem Ausgangspunkt. Diese Stelle kann nun im zweidimensionalen Bild genauso gut weiter hinten sein aber eben einfach höher oben auch. Es hängt wieder nur von der Umgebung und von der Darstellung des Wassers selbst ab. Wenn man das Wasser so darstellt dass man den Eindruck hat dass es senkrecht herunter fließt dann passt es natürlich mit der vorherigen Darstellung nicht zusammen. Man könnte das Wasser natürlich auch wieder entlang der zweiten strichlierten Linie nach vorne fließen lassen wie es im Bild rechts dargestellt ist, dann sieht alles wieder normal aus. Dass eine Linie nach rechts oben im zweidimensionalen Bild die Richtung von vorne nach hinten bedeutet entspricht einfach der Ansicht von oben rechts, was man in der Darstellung von Objekten sehr oft verwendet.
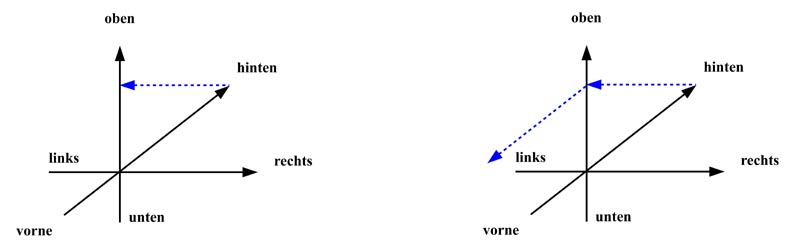
Bild 2
Man
kann es sich leicht veranschaulichen wenn man, wie im folgenden Bild 3 links dargestellt,
einen Sessel etwas von
oben ansieht. Ein Punkt an der Lehne ist höher oben, der daneben
liegende Punkt am Fußboden ist weiter hinten aber nicht
höher. Wenn man einen Gegenstand dreidimensional vor sich hat kann
man sich nicht täuschen, in der Projektion auf ein
zweidimensionales Bild aber
schon. Man bräuchte nur, wie im folgenden Bild rechts dargestellt, einen Übergang zwischen
Fußboden und Sessellehne malen, eventuell in gleicher Weise wie
beim Wasserfall. Ein Rinnsal entlang den Fußboden nach hinten
(blau)
und dann eine Querverbindung zur Sessellehne (blau strichliert). Und
schon kann das
Wässerchen die Sessellehne herunter, zum Rinnsal zurück,
fließen.

Bild 3
In einer Projektion des Zweidimensionalen auf das Dreidimensionale ist eben hinten unten von vorne oben nicht zu unterscheiden. Es hängt nur von der dargestellten Umgebung ab. Wenn man einen entsprechenden Übergang malt dann kann man auf diese Weise leicht eine optische Täuschung erzeugen.
An einem solchen Bild wie den Wasserfall ist also absolut nichts mysteriöses. Durch die Projektion der dritten Dimension (vorne hinten) auf die zwei Dimensionen des ebenen Bildes kann der gleiche Bildpunkt eben verschiedene Orte im dreidimensionalen Raum darstellen. Wenn man es darauf anlegt kann man damit optische Täuschungen darstellen. Mehr ist da nicht dahinter auch wenn es auf den ersten Blick etwas verwirrend erscheinen mag.

Bild 3
In einer Projektion des Zweidimensionalen auf das Dreidimensionale ist eben hinten unten von vorne oben nicht zu unterscheiden. Es hängt nur von der dargestellten Umgebung ab. Wenn man einen entsprechenden Übergang malt dann kann man auf diese Weise leicht eine optische Täuschung erzeugen.
An einem solchen Bild wie den Wasserfall ist also absolut nichts mysteriöses. Durch die Projektion der dritten Dimension (vorne hinten) auf die zwei Dimensionen des ebenen Bildes kann der gleiche Bildpunkt eben verschiedene Orte im dreidimensionalen Raum darstellen. Wenn man es darauf anlegt kann man damit optische Täuschungen darstellen. Mehr ist da nicht dahinter auch wenn es auf den ersten Blick etwas verwirrend erscheinen mag.
Verwandte Themen:
Räumliches Sehen
Das Spiegelbild
Startseite