Massenkräfte 1. Ordnung
Ein 3-Zylinder Reihenmotor weist die in Abb. 1 dargestellte Konfiguration des Kurbeltriebs auf. In diesem Bild sind auch die Massenkräfte 1. Ordnung der oszillierenden Massen eingezeichnet. Der Begriff der Massenkräfte 1. Ordnung ist beim Massenausgleich des 4-Zylinder Reihenmotors beschrieben.
 
 
 
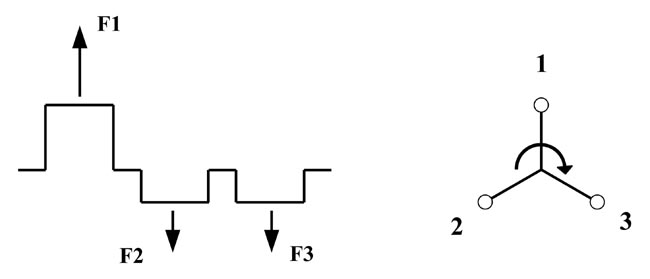
Abb. 1

Für die Kurbelwellenkonfiguration des 3-Zylinder Motors ergibt sich daher, über den Kurbelwinkel des 1. Zylinders aufgetragen, der in der folgenden Abb. 2 links dargestellte Verlauf der Massenkräfte 1. Ordnung für die drei Zylinder. Die Kräfte die in die beiden entgegengesetzten Richtungen wirken heben sich zu jeden Zeitpunkt auf, die resultierende Kraft ist null. Allerdings bewirken sie, wie man in Abb. 1 sieht, ein Moment um die Querachse zur Kurbelwelle.


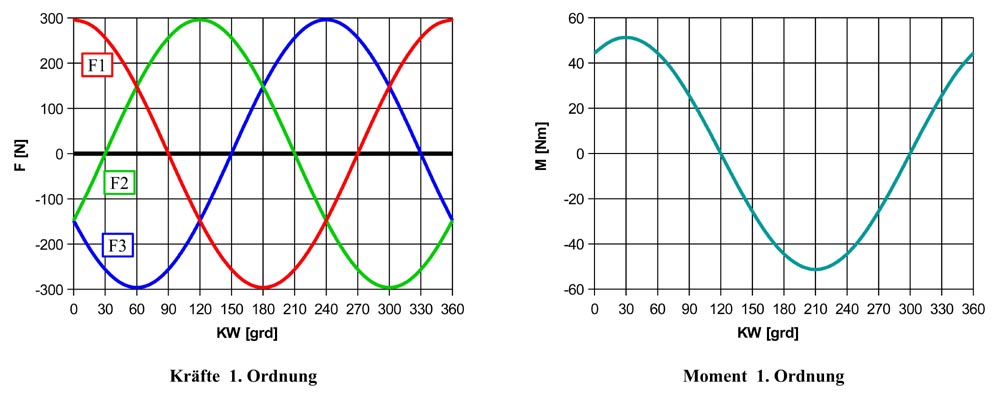
Abb. 2


Momente 1. Ordnung
In der folgenden Abb. 3 sieht man die kontinuierliche Veränderung der Massenkräfte 1. Ordnung durch die Drehbewegung, was sich entsprechend auf das entstehende Moment auswirkt.
Bei 0 Grad Kurbelwinkel wirkt die Kraft des 1 Zylinders nach oben, die Kräfte des Zylinders 2 und 3 wirken nach unten. Das ergibt ein rechtsdrehendes Moment von Größe: M = F2 . z + F3 . 2z (z = Zylinderabstand). Bis 30 Grad KW wird die Kraft F3 größer und die Kraft F2 kleiner, bei 30 Grad KW ist die Kraft F2 = 0. Das Moment ist dann F3 . 2z (bzw. F1. 2z). Die Summe der Kräfte die in die beiden entgegengesetzten Richtungen wirken werden zwar etwas kleiner (cos 30 = 0,87) aber der mittlere für das Moment verantwortliche Abstand wächst von 1,5z zu 2z. Bei 30 Grad KW ist daher das Moment am größten. Nach 30 Grad verhält sich der Verlauf des Moments spiegelbildlich, F1 wird zunehmend kleiner, F2 wird von null weg wieder zunehmend größer, bzw. anders ausgedrückt der mittlere für Moment verantwortliche Zylinderabstand wird von 2z bei 30 Grad wieder kontinuierlich kleiner zu 1,5z bei 60 Grad.
Bei 90 Grad ist der mittlere Zylinderabstand nur noch 1z, bei 120 Grad ergibt sich eine Symmetrie der wirkenden Kräfte und das Moment wird hier zu null. Bei 210 Grad ergibt sich ein maximales linksdrehendes Drehmoment, bei 300 Grad wird das Drehmoment wieder 0 und danach wieder rechtsdrehend.
Man sieht also das hier ein pulsierendes Moment entsteht das vor allem durch die ständig sich ändernde Konfiguration der Kraftwirkung der drei Zylinder entsteht. Die Summe der in die beiden entgegengesetzten Richtungen wirkenden Kräfte ändert sich dabei nur wenig. Alle 60 Grad wenn eine der 3 Kurbelkröpfungen sich im oberen oder unteren Totpunkt befindet,  bei 0, 60, 120, ... Grad besteht ein Maximum der Kräfte, dazwischen bei 30, 90, 150, ... Grad, wenn eine der 3 Kurbelkröpfungen horizontal ist, entsteht ein Minimum entsprechend dem cos von 30 Grad des Maximums.
Das entstehende Moment hat einen Verlauf wie in Abb. 2 rechts dargestellt (z = 100 mm). Der Verlauf dieses Moments entspricht tatsächlich wieder einer Sinuskurve und kann daher mit entsprechenden Massenausgleichswellen ausgeglichen werden.

Abb. 3


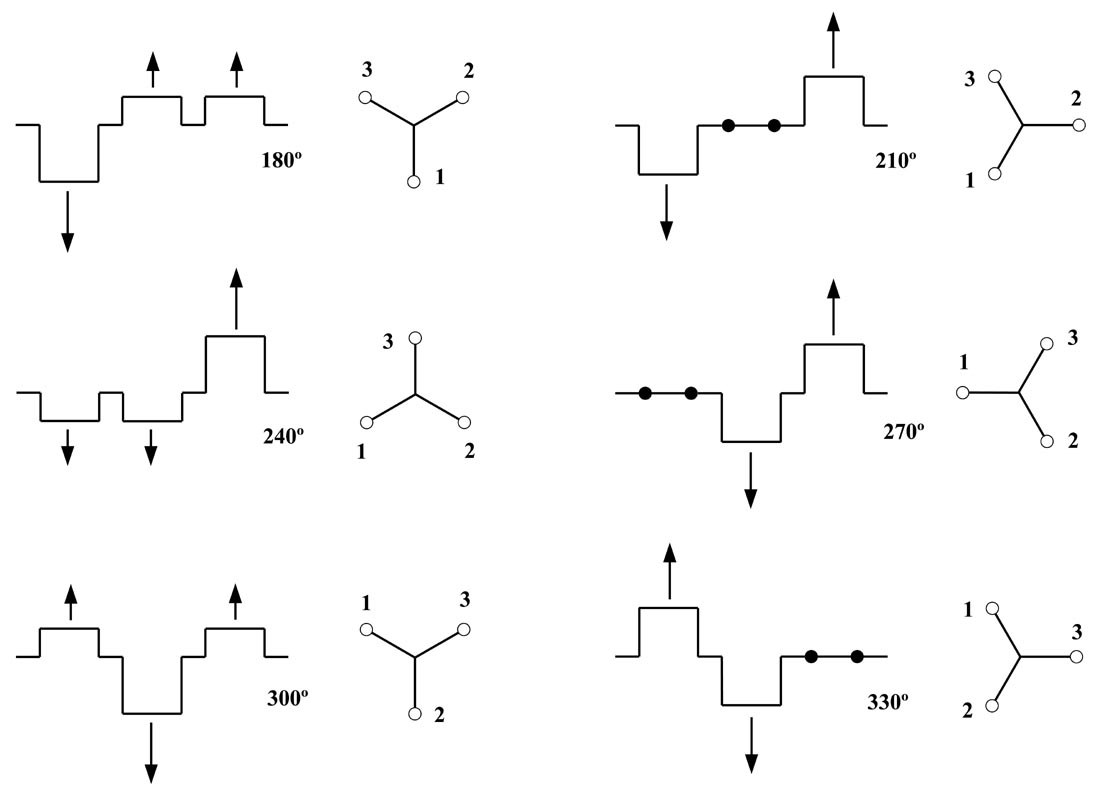
Ausgleich der Momente 1. Ordnung
Um dieses Moment vollständig auszugleichen braucht man zwei gegenläufige Massenausgleichswellen wie sie in der folgenden Abb. 4 dargestellt sind. Die horizontalen Kräfte bzw. die daraus resultierenden Momente heben sich auf, die vertikalen Kräfte bzw. die daraus resultierenden Momente beider Wellen addieren sich.
Da die Frequenz der 1. Ordnung der Kurbelwellendrehzahl entspricht kann man die Massen einer Welle bei den Gegengewichten der Kurbelwelle berücksichtigen. Man braucht daher zusätzlich zur Kurbelwelle nur eine weitere Massenausgleichswelle.
Da man ein Moment überall an einem Objekt ausgleichen kann besteht hier immerhin eine gewisse Freiheit wo man im Kurbelgehäuse die Massenausgleichswelle unterbringen will.




Wenn man sich den Aufwand für eine eigene Massenausgleichswelle sparen will bzw. es nicht für unbedingt notwendig hält kann man mit der Kurbelwelle auch nur einen Teil des Moments ausgleichen. Um den Betrag um den man das vertikale Moment reduziert handelt man sich dann allerdings ein horizontales Moment ein. Das kann aber, je nach Anwendung und Größe des Moments (Drehzahl) einen geeigneten Kompromiß darstellen.



Massenkräfte 2. Ordnung
Der Begriff der 2. Ordnung ist wieder beim Massenausgleich des 4-Zyliner Reihenmotors beschrieben.



Abb. 5


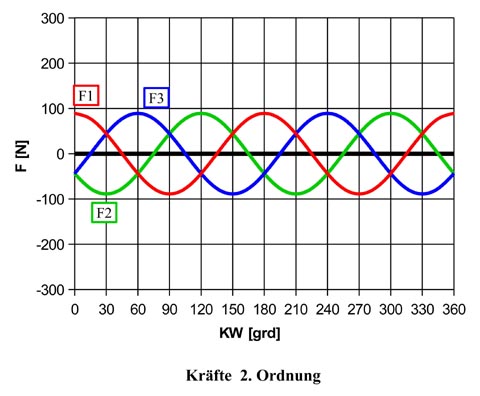
Die Massenkräfte 2. Ordnung verhalten sich beim 3-Zylinder Reihenmotor ganz analog wie die 1. Ordnung (Abb. 5). Die in beide Richtungen wirkenden Kräfte heben sich auch hier auf und es entsteht auch ganz analog ein Moment um die Querachse der Kurbelwelle. Allerdings pulsiert dieses Moment 2. Ordnung mit doppelter Frequenz. 
Da das Moment 2. Ordnung wesentlich kleiner ist, grob gesprochen etwa ein Drittel der 1. Ordnung (Pleuelverhältnis), und dafür auch zwei Massenausgleichswellen erforderlich sind, wird das Moment 2. Ordnung normalerweise nicht ausgeglichen. Allenfalls kann ein Ausgleich der 2. Ordnung bei sehr hochdrehenden Motoren notwendig sein.


Schlusspunkt
So, damit wäre nun im Prinzip der Massenausgleich des 3-Zylinder Reihenmotors auf möglichst anschauliche Weise dargestellt.

Die 3-Zylinder Reihenmotoren haben in letzter Zeit wieder an Bedeutung gewonnen da durch die Verringerung des Hubraums bei Turbomotoren, in PKWs mit kleineren Motorisierungen, nun auch wieder 3-Zylinder Motoren verwendet werden.



Darstellung von Momenten
Anzumerken wäre noch dass Momente häufig wie Vektoren, also wie z.B. Kräfte, dargestellt werden (Abb. 6). Die Darstellung des Moments als Vektor entspricht dabei der sogenannten Korkenzieherregel.





Abb. 6



Beim 3-Zylinder Reihenmotor würde diese Darstellung bedeuten dass die Momente mit einem Vektor, quer zur Kurbelwellenachse, dargestellt werden. Bei einem Drehmoment würde es bedeuten dass dieses Drehmoment als ein Vektor in Richtung der Wellenachse dargestellt wird.
Diese Darstellung hat den Vorteil dass damit Momente wie Vektoren, also wie z.B. Kräfte, einfach geometrisch zusammengesetzt werden können. Anschaulich ist diese Darstellung freilich nicht. Denn in die Richtung dieses Vektors wirkt ja überhaupt nichts sondern das Moment wirkt um diesen Vektor. Für die geometrische Zusammensetzung von Momenten ist diese Darstellung also gut geeignet, für die Veranschaulichung der Wirkung von Momenten ist diese Darstellung aber eher nicht geeignet.




Verwandte Themen

Massenausgleich des 4 Zyl. Reihenmotors

Drehmoment des Dieselmotors

Diesel FAQ

Das Drehmoment (Nm) und die Physikalische Arbeit (Nm)

Anti-Blockier-System




Zurück zu
Startseite


Copyright © 2018          Gottfried Langmann                   28.6.2018             aktualisiert:   16.5.2019