Bei einem 4-Zylinder Reihenmotor laufen jeweils zwei Kolben in die entgegengesetzte Richtung was auf den ersten Blick die Massenkräfte ausgleichen sollte.

Massenkräfte 1. und 2. Ordnung
Nun die Schrägstellung des Pleuels führt dazu dass die oszillierenden Massen, das sind der Kolben plus Pleuelanteil, im oberen Totpunkt größere Beschleunigungen aufweisen als im unteren Totpunkt.
In der folgenden Skizze sind die geometrischen Zusammenhänge dargestellt.
Würde das Pleuel senkrecht stehen so wäre der Kolbenweg in der oberen Hälfte, also 90 grd vor und nach dem oberen Totpunkt gleich wie in der unteren Hälfte also 90 grd vor und nach dem unteren Totpunkt (Weg a).
Aufgrund der Schrägstellung des Pleuels legt der Kolben aber in der oberen Hälfte mehr Weg zurück als in der unteren Hälfte (Weg b bzw. c). Mehr Weg der osz. Massen in der oberen Hälfte heißt aber auch mehr Geschwindigkeit und in der Folge mehr Beschleunigung in der oberen Hälfte. Da die Massenkraft direkt von der Beschleunigung abhängt bedeutet dies auch mehr Massenkraft in der oberen Hälfte.



Abb. 1   Kurbeltriebgeometrie



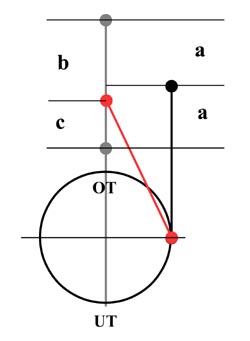
Stünde das Pleuel senkrecht, was natürlich nicht möglich ist, so entspräche die osz. Massenkraft einer reinen Sinuskurve. Durch die Schrägstellung des Pleuels ergibt dies aber eine Art verzerrte Sinuskurve.
Die theoretische Gleichung für diese Beschleunigung der osz. Massen lautet:

a = r.ω².[cosφ+λ.(cos(2φ)+λ².sin^4(φ))/ √((1-λ².sin²φ)³)]

a.....................Beschleunigung [m/s²]
r......................Kurbelradius [m]
ω = n.π/30.....Winkelgeschwindigkeit [rad/s]
n....................Drehzahl [U/min]
φ....................Kurbelwinkel [grd] bzw. [rad]
λ = r/l.............Pleuelverhältnis
l.....................Pleuellänge [m]

Allerdings kann man diese theoretische Kurve, wie jede andere Kurve auch, durch eine Überlagerung von einer Reihe von Sinuskurven darstellen. Bei dieser verzerrten Sinuskurve ist diese Darstellung sogar ausgesprochen einfach. Mit zwei Sinuskurven, eine Sinuskurve über 360 grd, man spricht von der 1. Ordnung, und eine Sinuskurve mit zwei Phasen über 360 grd, man spricht von der 2. Ordnung, ist die theoretische Kurve bereits sehr genau darstellbar.

Die 1. Ordnung ist:

a1 = r.ω².cosφ

Die 2. Ordnung ist:
 
a2 = r.ω².λ.cos2φ

Die Massenkraft der osz. Massen ergibt sich mit:

F = m.a

F.........Kraft [N]
m........Masse (Kolben + Pleuelanteil) [kg]


In der folgenden Grafik ist die 1. Ordnung grün dargestellt, die 2. Ordnung blau und die rote Kurve ist die Summe aus 1. und 2. Ordnung. Hinter der roten Kurve ist noch eine schwarze Kurve dargestellt die der theoretischen Kurve entspricht. Da aber die Darstellung mit zwei Ordnungen bereits sehr genau der theoretischen Kurve entspricht, ist der Unterschied in der Grafik praktisch nicht erkennbar. Zwei Ordnungen reichen hier also völlig aus um die theoretische Kurve mit großer Genauigkeit darzustellen, der Rest ist daher praktisch bedeutungslos.
Die größte Abweichung von einer reinen Sinuskurve besteht im oberen und unteren Totpunkt aber auch bei 90 und 270 grd in die Gegenrichtung wirkend.
Die in der Grafik als Beispiel verwendeten Kräfte beruhen auf einem Kurbelradius von 45 mm, einer Pleuellänge 150 mm (λ = 0,3), auf einer osz. Masse von 0,6 kg und einer Drehzahl 1000 U/min.




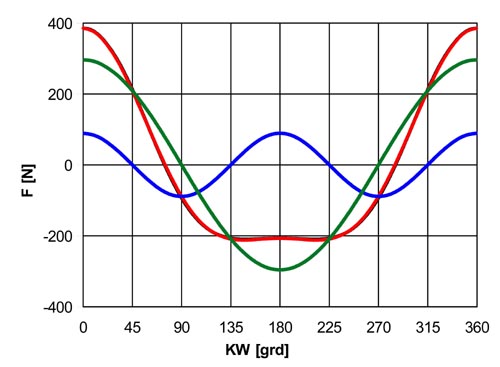
Abb. 2   Massenkraft eines Zylinders


Massenkräfte beim 4-Zylinder Reihenmotor
Bei einem 4-Zylinder Reihenmotor sind die Kolben der beiden inneren Zylinder um 180 grd versetzt zu den Kolben der beiden äußeren Zylinder. In der linken der nächsten beiden Grafiken sind die Massenkräfte 1. Ordnung für alle 4 Zylinder eingetragen. Die Massenkräfte jeweils zweier Zylinder addieren sich, die Massenkräfte der beiden anderen Zylinder wirken in die Gegenrichtung. Insgesamt heben sich die Massenkräfte 1. Ordnung auf. Dies ergibt sich auch aus dem Umstand dass die Massenkräfte 1. Ordnung der Massenkraft der reinen Sinuskurve eines theoretisch senkrecht stehenden Pleuels entspricht.
Bei der 2. Ordnung, wie in der rechten der beiden folgenden Grafiken dargestellt, bewirkt eine Versetzung jeweils zweier Zylinder um 180 grd dass die Massenkräfte 2. Ordnung aller 4 Zylinder gleichzeitig wirken, das heißt die Massenkräfte 2. Ordnung aller 4 Zylinder addieren sich. Dies ergibt sich auch aus dem Umstand dass die 2. Ordnung ja dem Unterschied der verzerrten theoretischen Sinuskurve zu einer reinen Sinuskurve entspricht.




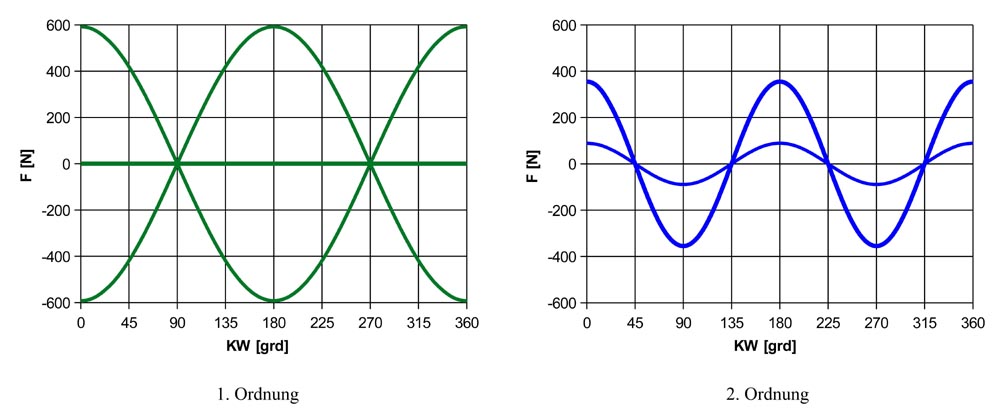
Abb. 3   Massenkräfte durch 4 Zylinder



Diese Summe der Massenkräfte 2. Ordnung bleibt also als freie Kraft erhalten. Da sich diese Massenkraft für alle 4 Zylinder addiert kann sie sich je nach Größe der Massen und je nach Drehzahl durchaus bemerkbar machen.

Massenausgleichswellen 2. Ordnung
Diese freie Massenkraft 2. Ordnung kann man mit zwei gegenläufigen Massenausgleichswellen, die sich mit doppelter Kurbelwellendrehzahl drehen, ausgleichen. Zwei gegenläufige Wellen sind deshalb notwendig weil ja sonst auch eine horizontale Massenkraft entstehen würde. Bei zwei gegenläufigen Wellen gleicht sich jedoch der horizontale Anteil aus, während sich der vertikale Anteil addiert.





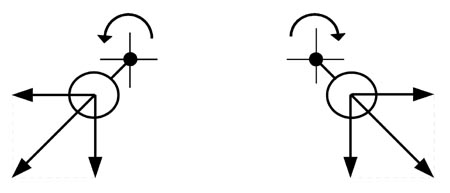
Abb. 4   Massenausgleichswellen 2. Ordnung



Die Massenausgleichswellen müssen links und rechts der Kurbelwelle angebracht werden da die resultierende senkrechte Massenkraft der beiden Wellen in der Mitte der Kurbelwelle wirken muss, wo auch die resultierende Massenkraft der osz. Massen wirkt. Auch in der Längsrichtung des Motors muss die resultierende Massenkraft der Ausgleichswellen in der Mitte der Kurbelwelle wirken. Man würde sonst ein Moment erzeugen.

Solche Massenausgleichswellen 2. Ordnung finden sich übrigens nicht nur bei PKW Motoren. Selbst Traktormotoren haben teilweise diese Massenausgleichswellen 2. Ordnung. Dort besteht zwar nicht der gleiche Komfortanspruch, bei Traktormotoren ist aber im Allgemeinen der Motorblock Teil der tragenden Struktur, die Schwingungen des Motors übertragen sich dort also direkt auf die tragende Struktur. Durch das große Gewicht der Struktur ist dort die Wirkung der Schwingungen allerdings nicht so stark.

Kurbelstern 1. und 2. Ordnung
Die Massenkraft der osz. Massen kann bei Motoren generell als Überlagerung der 1. und 2. Ordnung betrachtet werden. Bei geometrischer Darstellung spricht man von einem Kurbelstern 1. Ordnung der dem tatsächlichen Kurbelwinkel entspricht und einem Kurbelstern 2. Ordnung der dem doppelten Kurbelwinkel der jeweiligen Kurbelkröpfung entspricht.

Die Kurbelsterne 1. und 2. Ordnung des 4-Zylinder Reihenmotors sehen daher folgendermaßen aus:





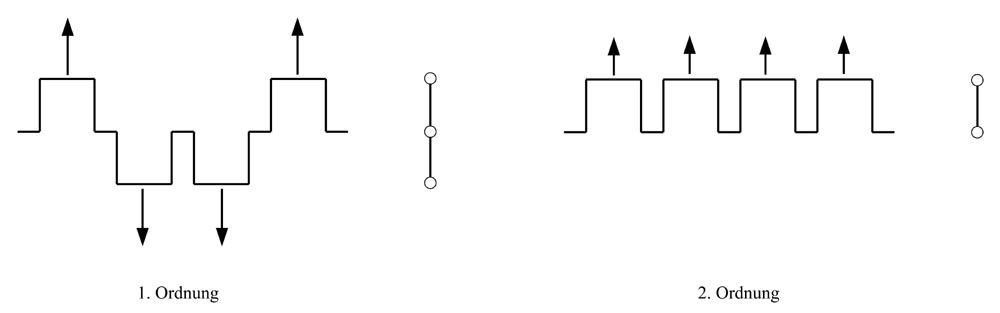
Abb. 5    Kurbelstern



Mit einer solchen geometrischen Darstellung sind die Kraftverhältnisse durch die osz. Massen gut zu erkennen.

Massenausgleich beim 1-Zylinder Motor
Will man im einfachsten Fall die osz. Massen eines 1-Zylinder Motors vollständig ausgleichen so braucht man zwei Wellen für die 1. Ordnung und zwei Wellen für die 2. Ordnung.
Auch hier müssen die Massenausgleichswellen auf beiden Seiten der Kurbelwelle angeordnet sein sodass die resultierende Wirkung der Massenausgleichswellen in die Zylinderachse fällt. Auch in Längsrichtung des Motors müssen die Massenausgleichswellen in der Zylinderachse wirken. Sonst würde ein Moment entstehen.

Rotierende Massen
Rotierende Massen kann man dagegen bei jedem Motor, ob 1-Zylinder oder Mehrzylinder, direkt mit Gegengewichten an der Kurbelwelle ausgleichen.

Ordnungen durch die Verbrennung
Anzumerken wäre noch dass sich der Gasdruck durch die Verbrennung auch durch eine Reihe von Ordnungen darstellen lässt. Dies ist aber etwas ganz anderes. Die Ordnungen des Verbrennungsdrucks wirken sich auf den Rundlauf des Motors aber auch auf die Drehschwingungen der Kurbelwelle aus.
Da beim 4-Zylinder 4-Takt Motor zwei Verbrennungen pro Kurbelwellenumdrehung stattfinden spielt hier die 2. Motor-Ordnung (0,5 Ordnung der einzelnen Zylinder) eine wesentliche Rolle.




Verwandte Themen

Massenausgleich beim 3-Zylinder Reihenmotor

Drehmoment des Dieselmotors

Diesel FAQ

Das Drehmoment (Nm) und die Physikalische Arbeit (Nm)

Anti-Blockier-System

Frontantrrieb  - Heckantrieb




Zurück zu
Startseite


4.7.2015               aktualisiert: 12.10.2019

Copyright © 2015          Gottfried Langmann